▶ AVL 트리 란?
- 이진 탐색 트리의 한 종류
- 스스로 균형을 잡는 트리
- balance factor 를 통해 균형 유지
▶ 노드의 balance factor 란?
- 임의의 노드 x 에 대해서 왼쪽 서브 트리의 높이와 오른쪽 서브트리의 높이의 차 이다.
- 균형 인수(balance factor)의 절댓값이 크면 클수록 그만큼 트리의 균형이 무너진 상태이다.
▶ AVL 트리의 특징
- 트리의 모든 노드들은 아래와 같은 특징을 갖는다
BF(x) ∈ { -1,0,1 }
- AVL 트리는 균형 인수의 절댓값이 2 이상인 경우 균형을 잡기 위한 트리의 재조정을 진행한다.
예를 들어 아래와 같은 이진 트리가 있을 때
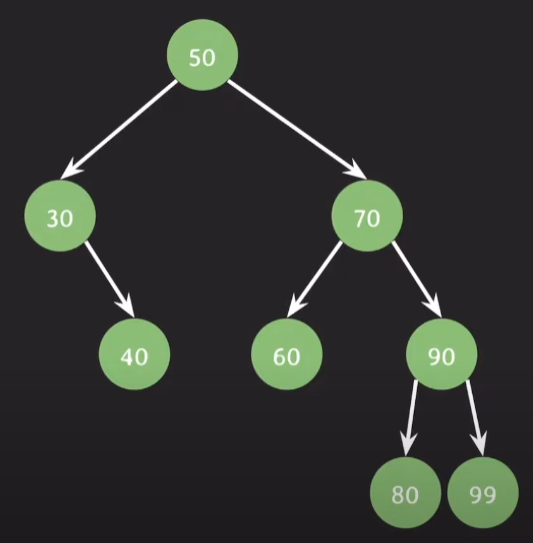
노드 50 은 왼쪽 서브 트리의 높이가 1 이고 오른쪽 서브 트리의 높이가 2 이기 때문에 -1 의 balance factor 값을 갖는다.

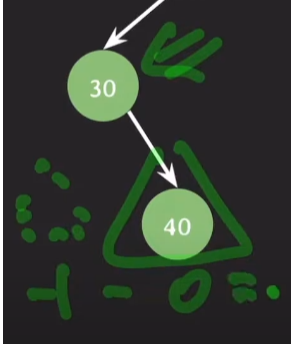
노드 30 은 왼쪽 서브 트리가 없으므로 높이가 -1 이고 오른쪽 서브트리는 높이가 0 이므로 -1-0 = -1의 값을 갖는다.
노드 70은 왼쪽 서브 트리의 높이가 0 이고 오른쪽 서브 트리의 높이가 1 이므로 0-1 = -1 의 값을 갖는다.

노드 90 은 왼쪽 서브트리와 오른쪽 서브트리의 높이가 모두 0이므로 0의 balance factor 값을 갖는다.

따라서 아래 이진 트리는 각 노드의 balance factor 가 { -1,0,1 } 이므로 AVL 트리라는 것을 알 수 있다.

▶ AVL 트리의 균형 잡기
트리에 삽입 혹은 삭제 후 balance factor 의 절댓값이 2 이상인 노드가 생기면 균형을 맞추는 작업을 수행한다.
insert(50)
insert(70)
insert(90) 을 하고나서 노드의 balance factor 의 값을 보면
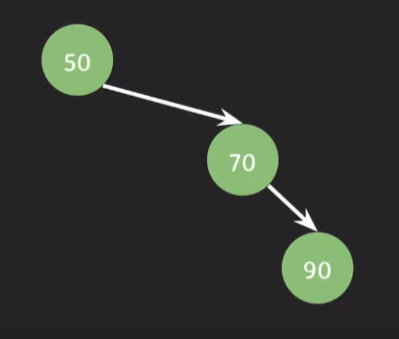
BF(70) = -1 - 0 = -1
BF(50) = -1 - 1 = -2
이므로 50을 기준으로 오른쪽 오른쪽으로 편향된 상태이다.

이럴 경우 70을 위로 올려준다.
insert(20) 을 하고나서 노드의 balance factor 의 값을 보면
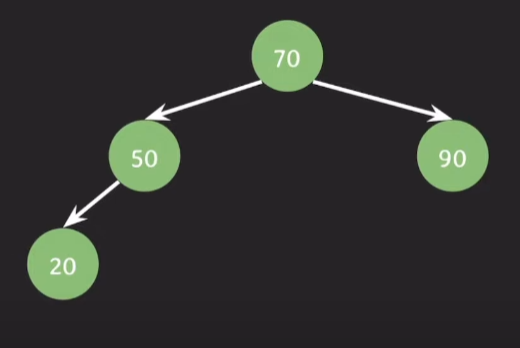
BF(50) = 0 - (-1) = 1
BF(70) = 1 - 0 = 1
이므로 AVL 트리의 조건을 만족한다.
insert(60) 을 하고나서 노드의 balance factor 의 값을 보면

BF(50) = 0 - 0 = 0
BF(70) = 1 - 0 = 1
이므로 AVL 트리의 조건을 만족한다.
insert(30) 을 하고나서 노드의 balance factor 의 값을 보면
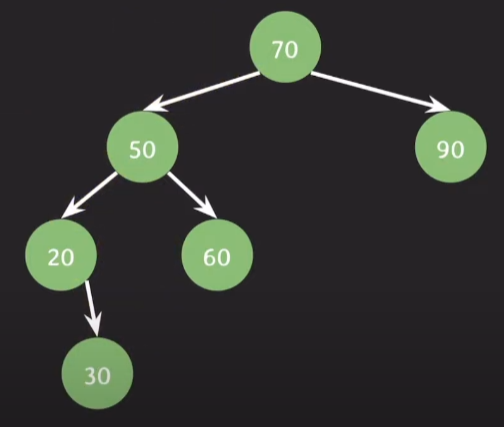
BF(20) = -1 - 0 = -1
BF(50) = 1 - 0 = 1
BF(70) = 2 - 0 = 2
이므로 70을 기준으로 왼쪽 왼쪽으로 편향된 상태이다.
이럴 경우 50을 70 위로 올리고
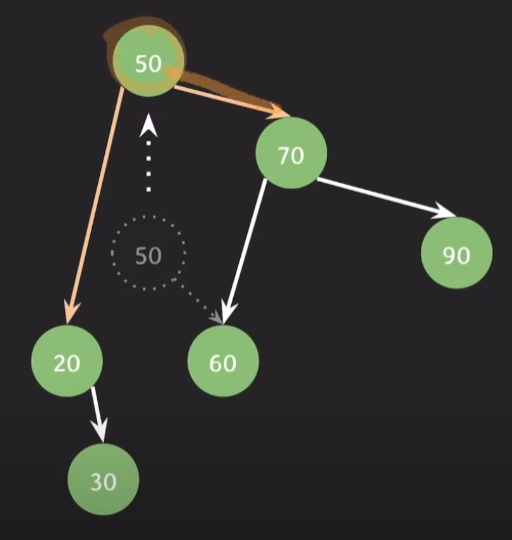
50의 오른쪽 자식이였던 60은 70의 왼쪽 자식이 된다.
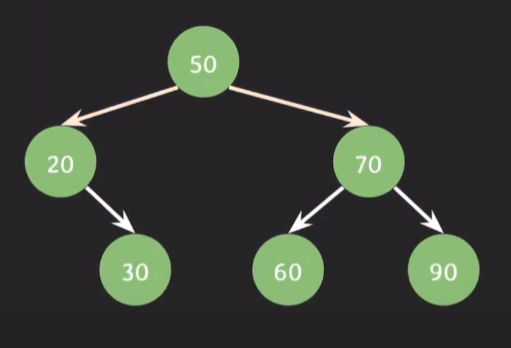
그리고 delete(20) 을 하게 되면

BF(30) = -1 - (-1) = 0
BF(50) = 0 - 1 = -1
이므로 AVL 트리의 조건을 만족하게 된다.
▶ 이렇듯 AVL 트리는 노드의 balance factor 의 절댓값이 2 이상이 넘어가는 순간 리밸런싱을 통해 한쪽으로 편향되지 않도록 한다.
'CS > 자료구조' 카테고리의 다른 글
| AVL 트리 연습용 예제 (0) | 2024.04.04 |
|---|---|
| 자료구조 - 해쉬테이블 (0) | 2024.02.03 |
| 자료구조 - 이진탐색트리 (1) | 2024.01.31 |
| 자료구조 - 보간 탐색 (0) | 2024.01.26 |
| 자료구조 - 퀵 정렬 (0) | 2024.01.26 |
